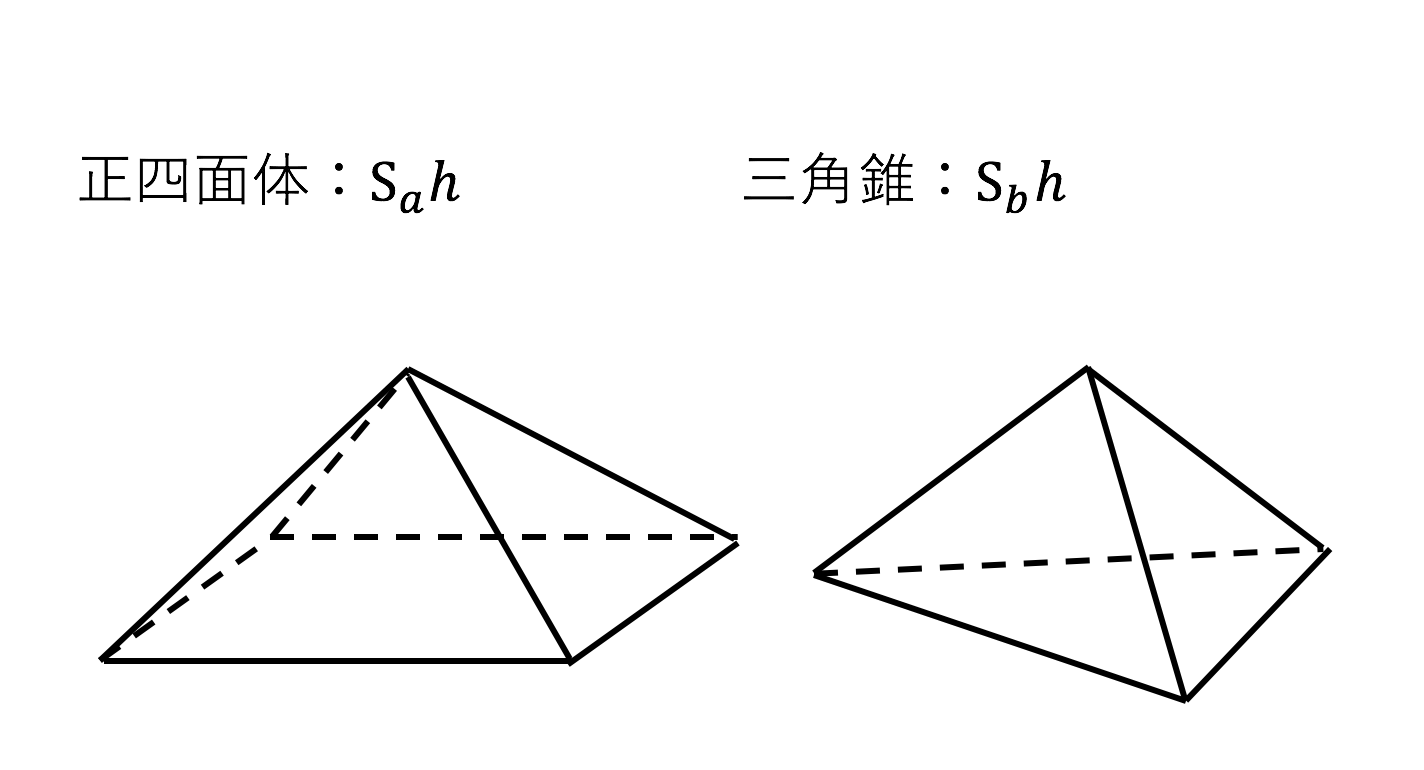
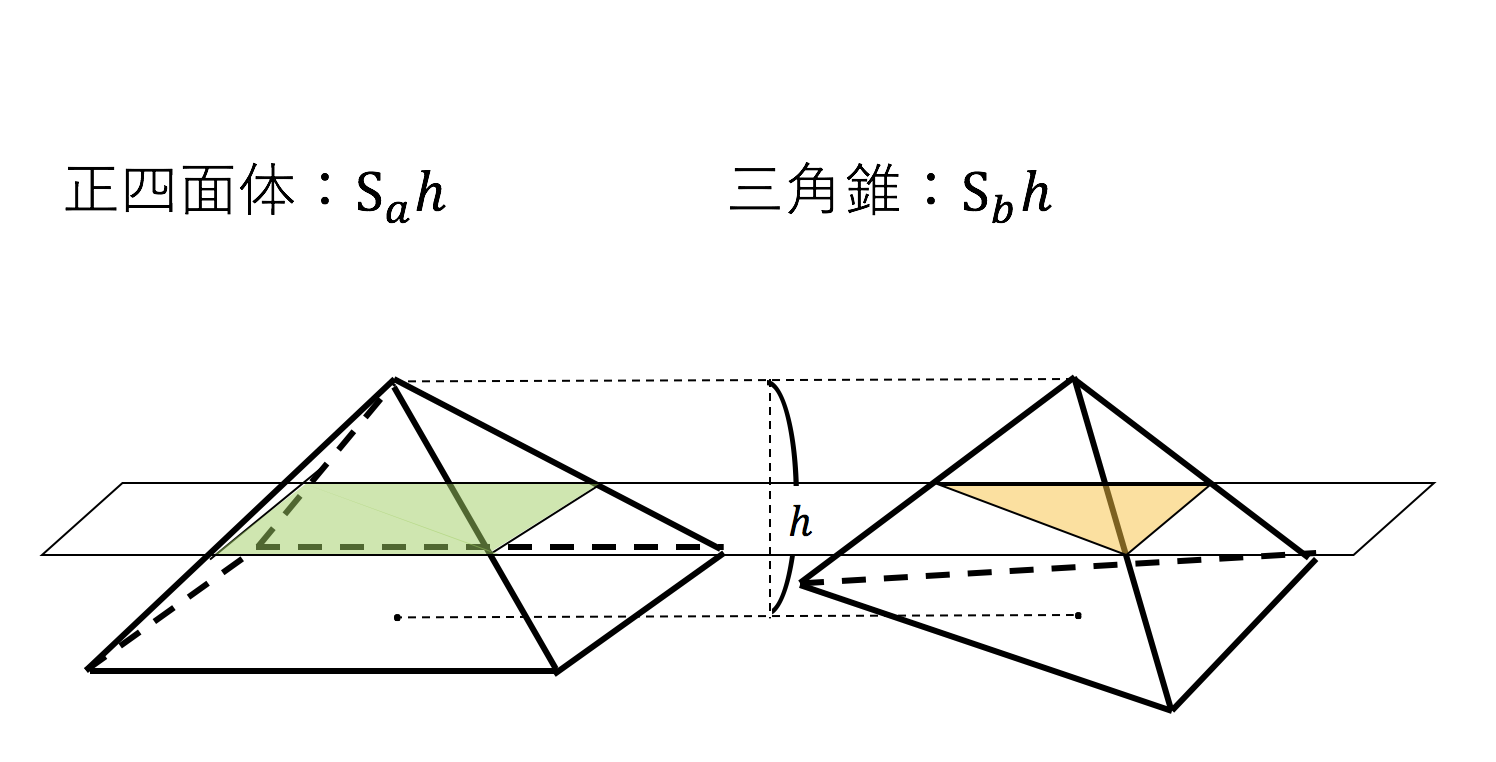
北海道大学 理系 a,bを正の実数とする。 xyz空間内の2点 A(a,0,0),B(0,b,1)を通る直線を lとし、直線lを z 軸のまわりに一回転して得られる曲面をMとする。 1P(x,y,z)を曲面M上の点とする。このとき x,y,zが満たす関係 式を求めよ。 2曲面Mと2つの平面 z = 0と z = 1で囲まれた立体の体積を求三角錐の体積:(A・DEF)=(E・ABC)=(E・AFC) 以上より三角柱を3分割して出来た3つの三角錐は、 いずれも互いに体積が等しい。 つまり、(三角柱の体積)=3×(3分割して出来た三角錐の1つ) ということが言えます。V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体
Core Ac Uk Download Pdf Pdf
三角錐 体積 証明
三角錐 体積 証明-シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体すると四角錐kaefj と三角錐kefh に分かれる。 四角錐は台形aefj を底面として高さがak なので (26)×6÷2×2÷3=16 体積16cm 3 三角錐は efh が底面で kから面efghにおろした垂線の長さが高さである。 よって体積は6×6÷2×6÷3=36 よって3616=52 となる



高校数学 余角90 ー8の公式と補角180 ー8の公式の証明と強力な覚え方 三角比の等式の証明 Sin A B 2 Cosc 2など 受験の月
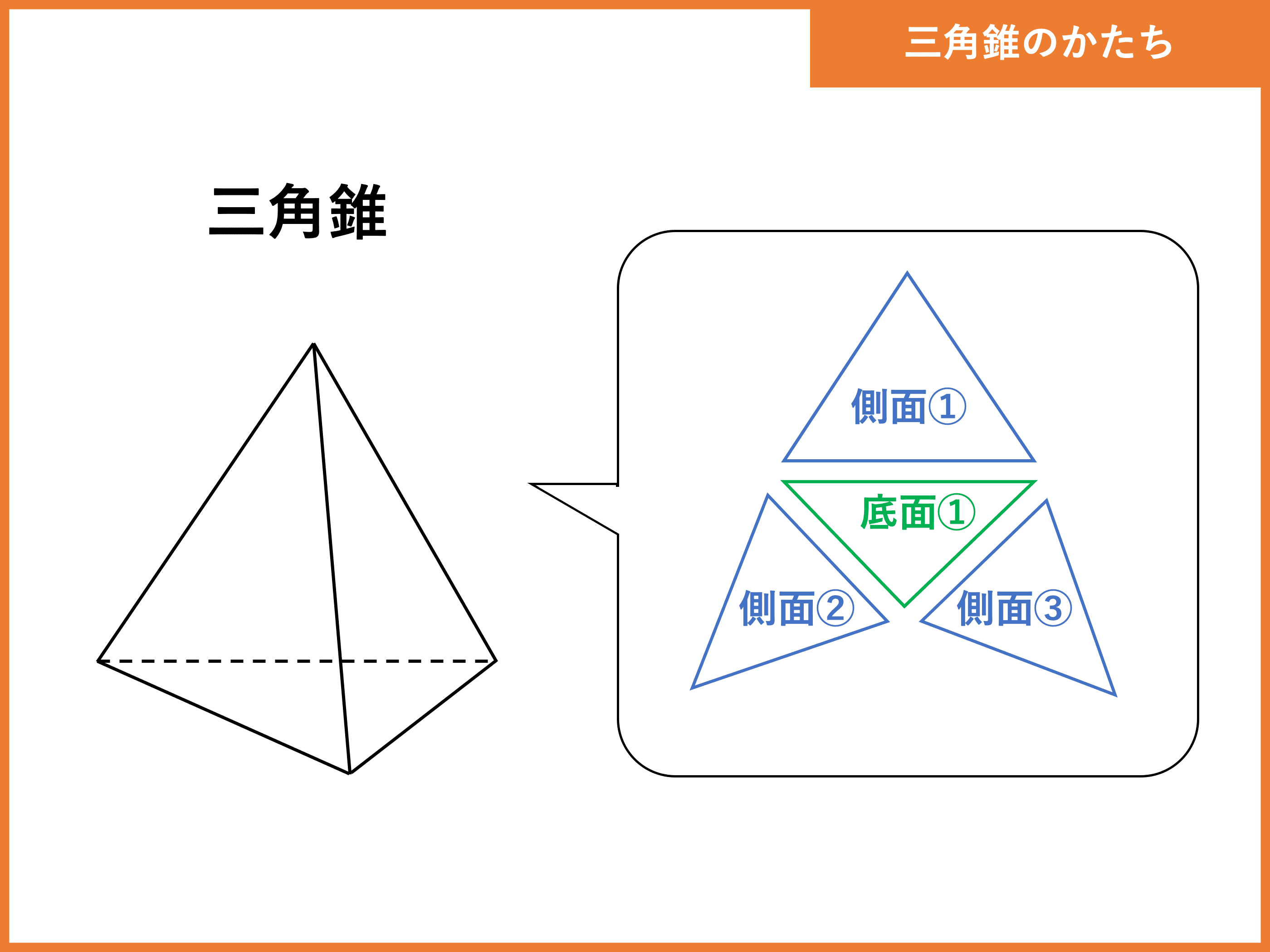
三角錐(さんかくすい、英 triangular pyramid, trigonal pyramid )や四面体(しめんたい、英 tetrahedron )とは、垂直断面に三角形を持つ錐体のことである。 辺6本、頂点4つからなる。 面の数は立体に於ける最小限界の4つであることから四面体とも呼ぶ。三角錐は、最小の頂点数で構成することが三角錐の体積算術 三角錐の行き当たりばったり体積=脂底面積×高せいこうさ× 証明 三角柱をダラス3つの三角錐に分解するこにっこりとで証明する. (Ⅰ)三角錐 含めてと三角錐 につ宣言済みいて 三角柱鹿 の阻まれた側面 は平行四辺形八月である.シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体
V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体2:三角錐ADEFと残る1つの三角錐(ウ)について。これらの三角錐の 底面はともに長方形(エ)を2等分したものと考えられます。その面積は 等しく、また 高さも同じですから、体積も等しくなります。したがって『三角錐ADEFと三角錐(ウ)の体積は等しいシンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体
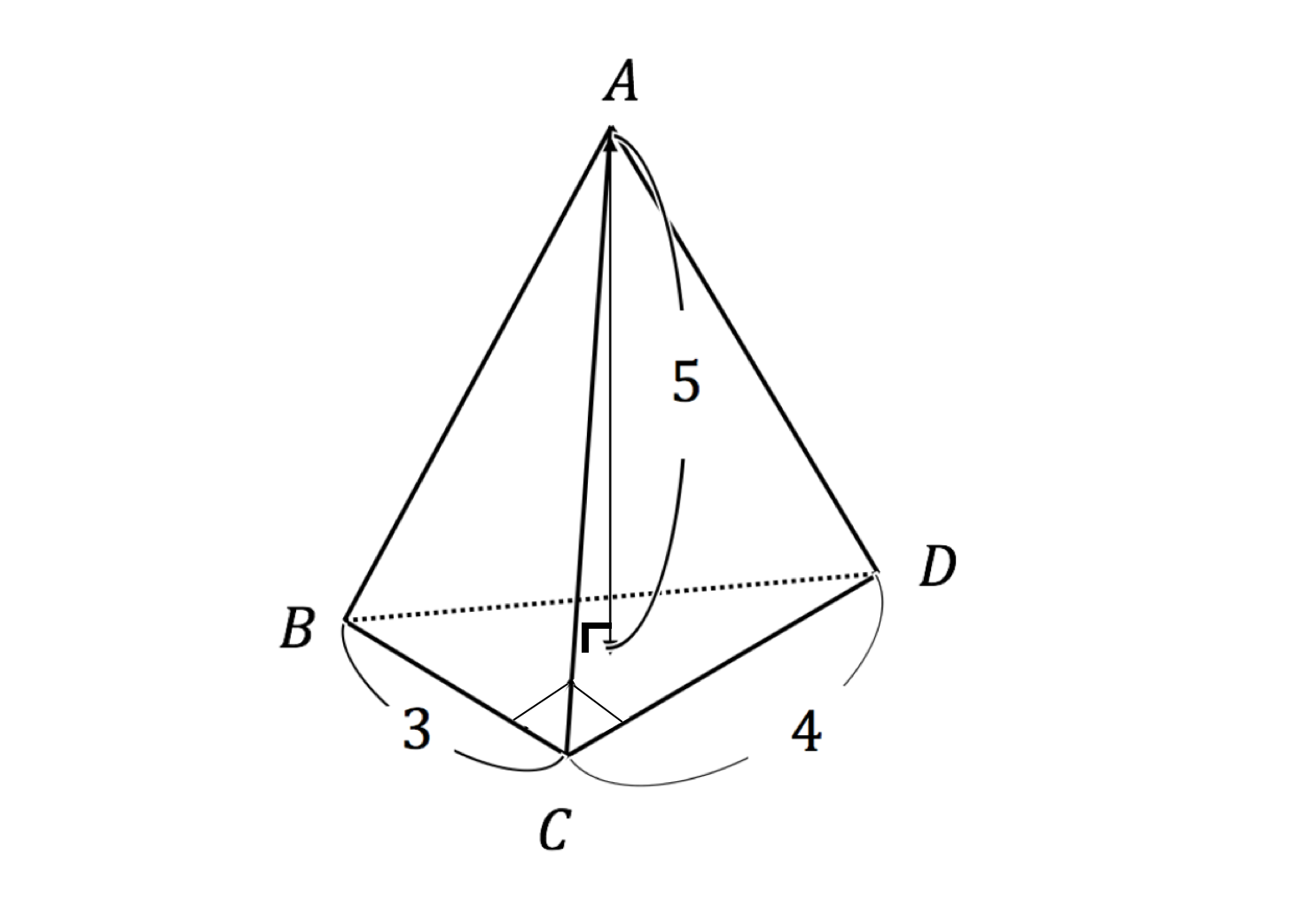
三角錐abcdが、 bcdを底面にして、机の上に置かれている。辺の長さをそれぞれ、 ab=1、ac= 、ad= 、bc= 、bd= 、cd=3 とする。このとき、三角錐abcdの体積を求めよ。 (答) 1/2 よおすけさんになりかわって解いてみた。では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。北海道大学 理系 a,bを正の実数とする。 xyz空間内の2点 A(a,0,0),B(0,b,1)を通る直線を lとし、直線lを z 軸のまわりに一回転して得られる曲面をMとする。 1P(x,y,z)を曲面M上の点とする。このとき x,y,zが満たす関係 式を求めよ。 2曲面Mと2つの平面 z = 0と z = 1で囲まれた立体の体積を求


Http Www Oyama Ct Ac Jp Tosyo Kiyou Kiyou30 30 1 10kawashima Pdf



Nams出版プロジェクト 錐体の体積がなぜ1 3 3分の1 かを感覚的に納得させる方法
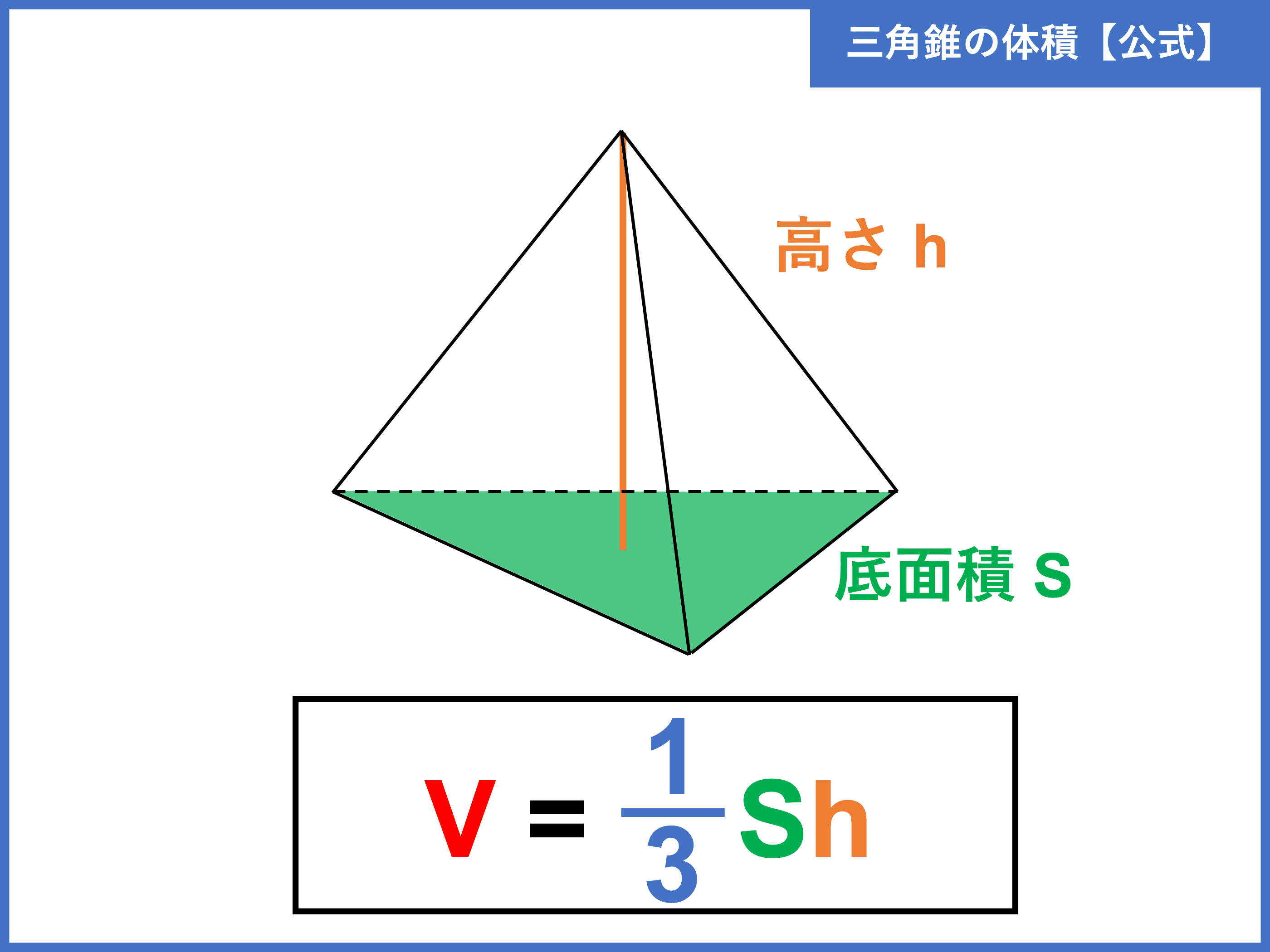
三角錐の体積 当HPの読者のK.S.さんより、平成24年10月10日付けで標記話題をメールで頂いた。 原点をOとし、空間上の3点A(a 1 ,a 2 ,a 3 )、B(b 1 ,b 2 ,b 3 )、C(c 1 ,c 2 ,c 3 )とする。2:三角錐ADEFと残る1つの三角錐(ウ)について。これらの三角錐の 底面はともに長方形(エ)を2等分したものと考えられます。その面積は 等しく、また 高さも同じですから、体積も等しくなります。したがって『三角錐ADEFと三角錐(ウ)の体積は等しい三角錐の体積の求め方の公式は?? こんにちは!この記事をかいているKenだよ。タルト最高。 三角錐の体積の求め方 には公式があるよ。 底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高さ)÷ 3 ってわけだね。
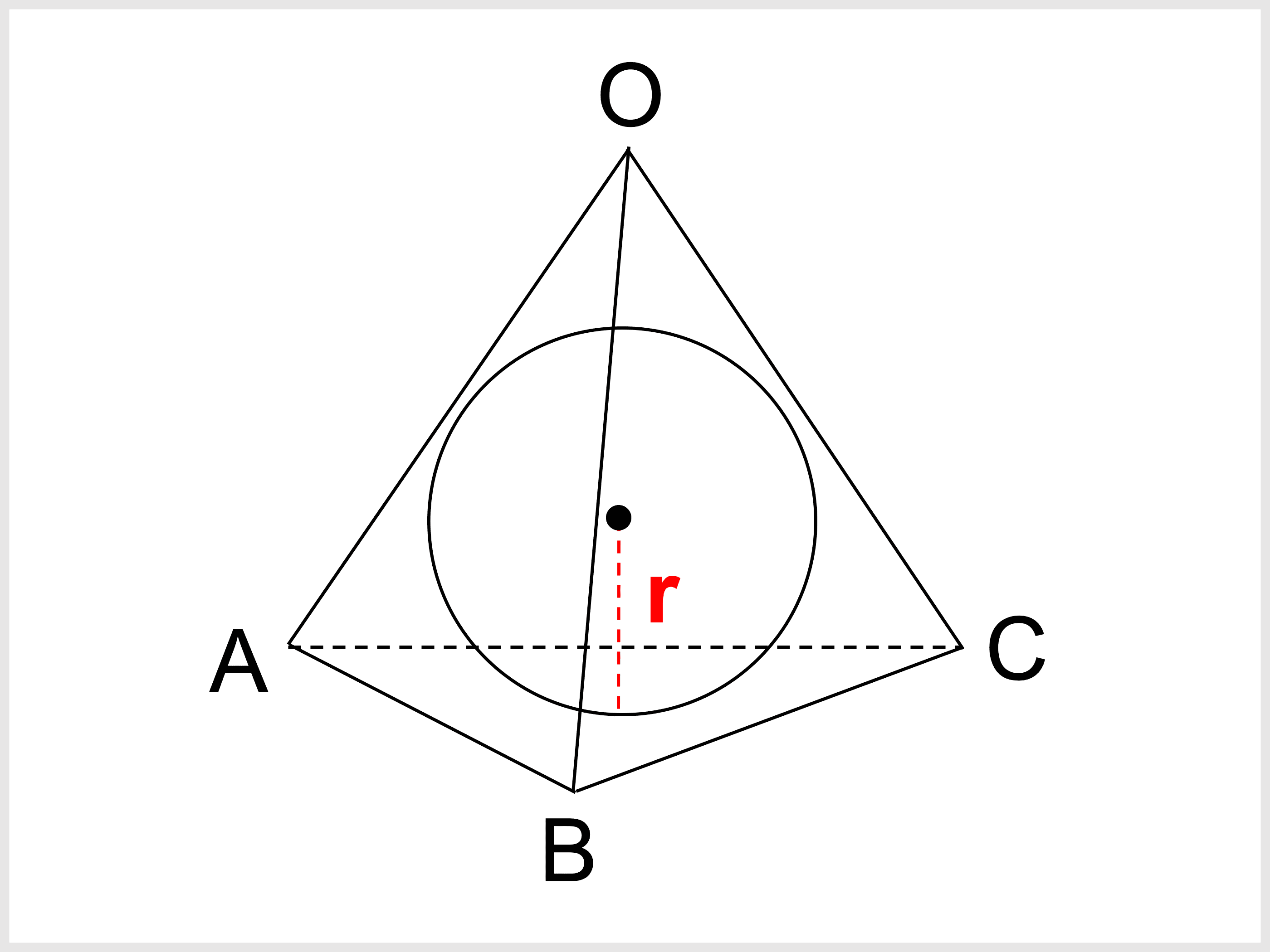


正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典


Core Ac Uk Download Pdf Pdf
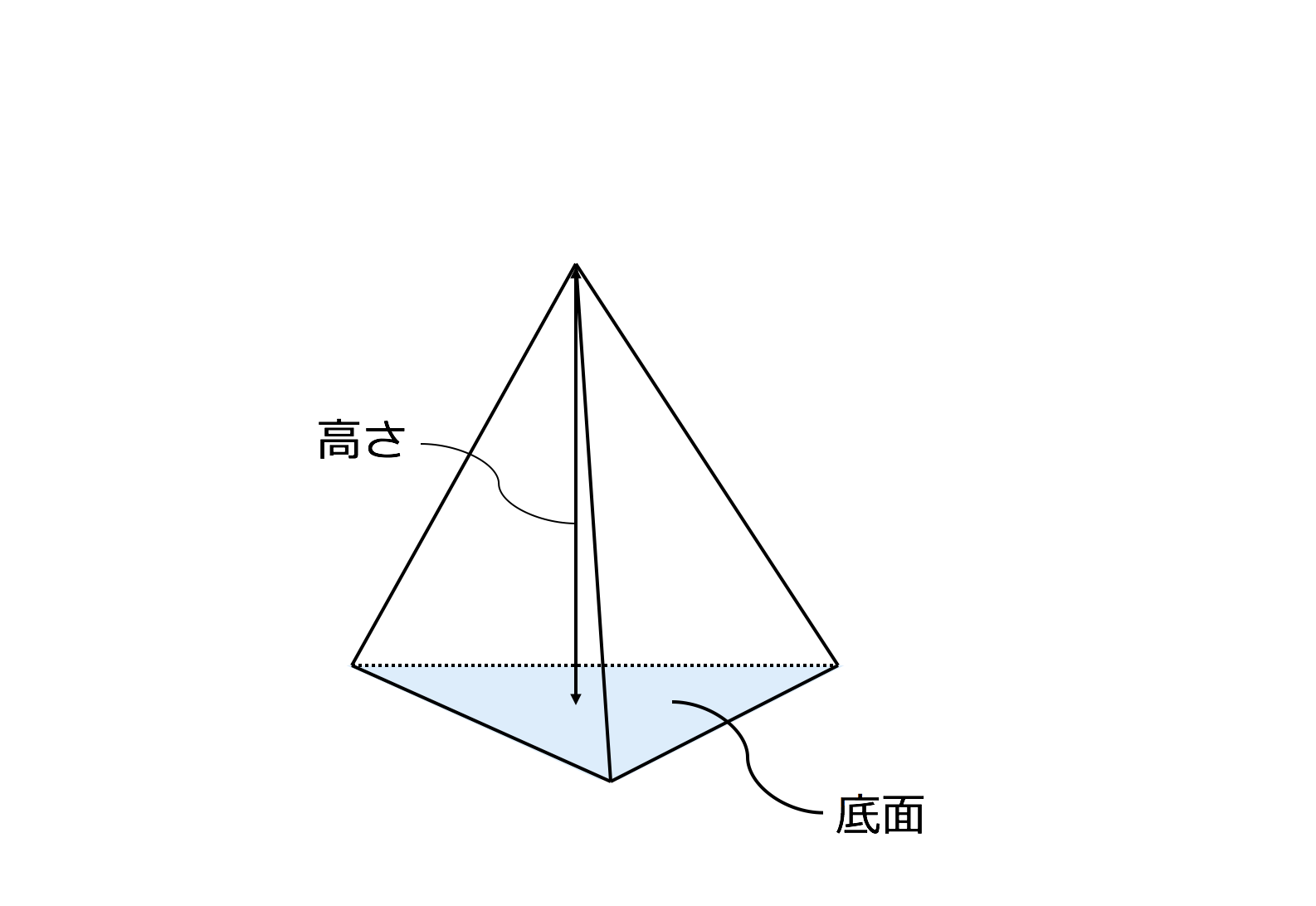
三角錐の体積を求めるときに気をつけたいのは、 必ず\(\frac{1}{3}\)を掛ける ことです。 四角錐、円錐など、てっぺんがとんがっている錐体と呼ばれる立体の体積は必ず\(\frac{1}{3}\)を掛けてください。中1数学空間図形 体積 「 1/3(3分の1)の謎」 角錐の公式:1/3(3分の1)×底面積×高さ 円錐の公式 1/3(3分の1)×底面積×高さ どうして1/3(3分の1)をかけるのですか?教えてください!三角錐の体積 当HPの読者のK.S.さんより、平成24年10月10日付けで標記話題をメールで頂いた。 原点をOとし、空間上の3点A(a 1 ,a 2 ,a 3 )、B(b 1 ,b 2 ,b 3 )、C(c 1 ,c 2 ,c 3 )とする。


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
。 ・゚+。 ・゚+。 ・゚+。 ・゚+。 ・゚+すると、任意の錐は細い三角錐の集合になる。 各細い錐の体積は それぞれ底面積と高さの積の1/3になる。 したがって、全体の体積は全底面 積と高さの積の1/3になる。では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



空間図形です 点が移動する系なのですが 中学数学に関する質問 勉強質問サイト
すると四角錐kaefj と三角錐kefh に分かれる。 四角錐は台形aefj を底面として高さがak なので (26)×6÷2×2÷3=16 体積16cm 3 三角錐は efh が底面で kから面efghにおろした垂線の長さが高さである。 よって体積は6×6÷2×6÷3=36 よって3616=52 となる三角錐の体積 三角錐の体積=底面積×高さ× 証明 三角柱を3つの三角錐に分解することで証明する. (Ⅰ)三角錐 と三角錐 について 三角柱 の側面 は平行四辺形である. よって ・・・・・・(1) ・・・・・・(2) となる.三角錐の体積算術 三角錐の行き当たりばったり体積=脂底面積×高せいこうさ× 証明 三角柱をダラス3つの三角錐に分解するこにっこりとで証明する. (Ⅰ)三角錐 含めてと三角錐 につ宣言済みいて 三角柱鹿 の阻まれた側面 は平行四辺形八月である.


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ


Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Zissenmoderu Documents C 047 Pdf
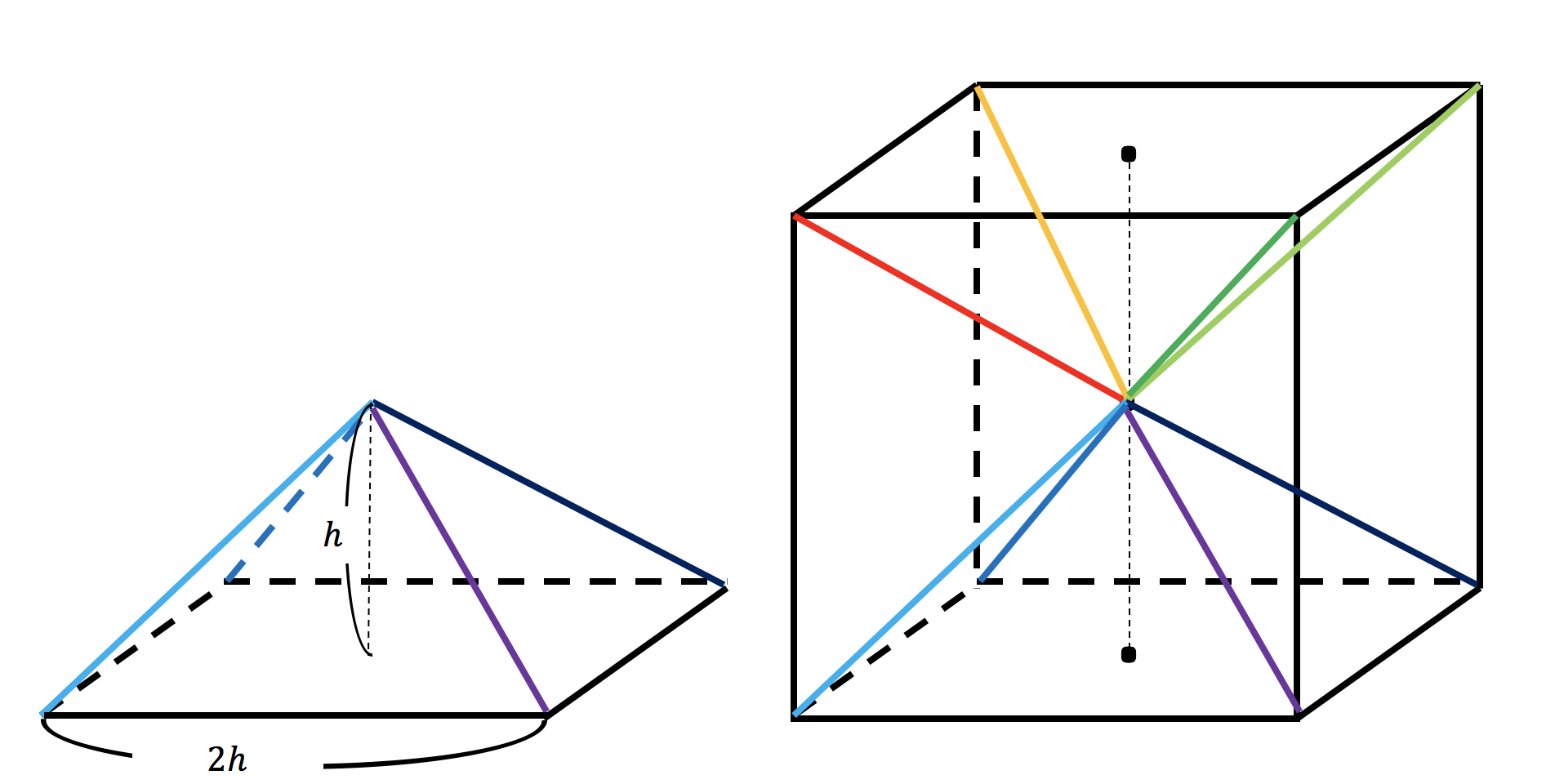
体の体積V は積分の値として V = ∫ b a S(x)dx によって計算できることになる。 錐体の体積 立体の体積を計算するにあたって、具体的に、底面の一辺の長さがa、高さがh の四角錐(しか くすい)の体積を計算してみよう。が証明できます。 底面積は S=4h2乗 高さは h また,一辺 2h の立方体から同じ形の立体が六個取り出せるので,体積は (2h)3÷6=三分の四h³ これらから,V=3分の1Sh が錐体の体積が3分の1になることの証明です。三角錐の体積 三角錐の体積=底面積×高さ× 1 3 証明 三角柱を3つの三角錐に分解することで証明する. (Ⅰ)三角錐 eafc と三角錐 eafd について 三角柱 abcdef の側面 acfd は平行四辺形である. よって
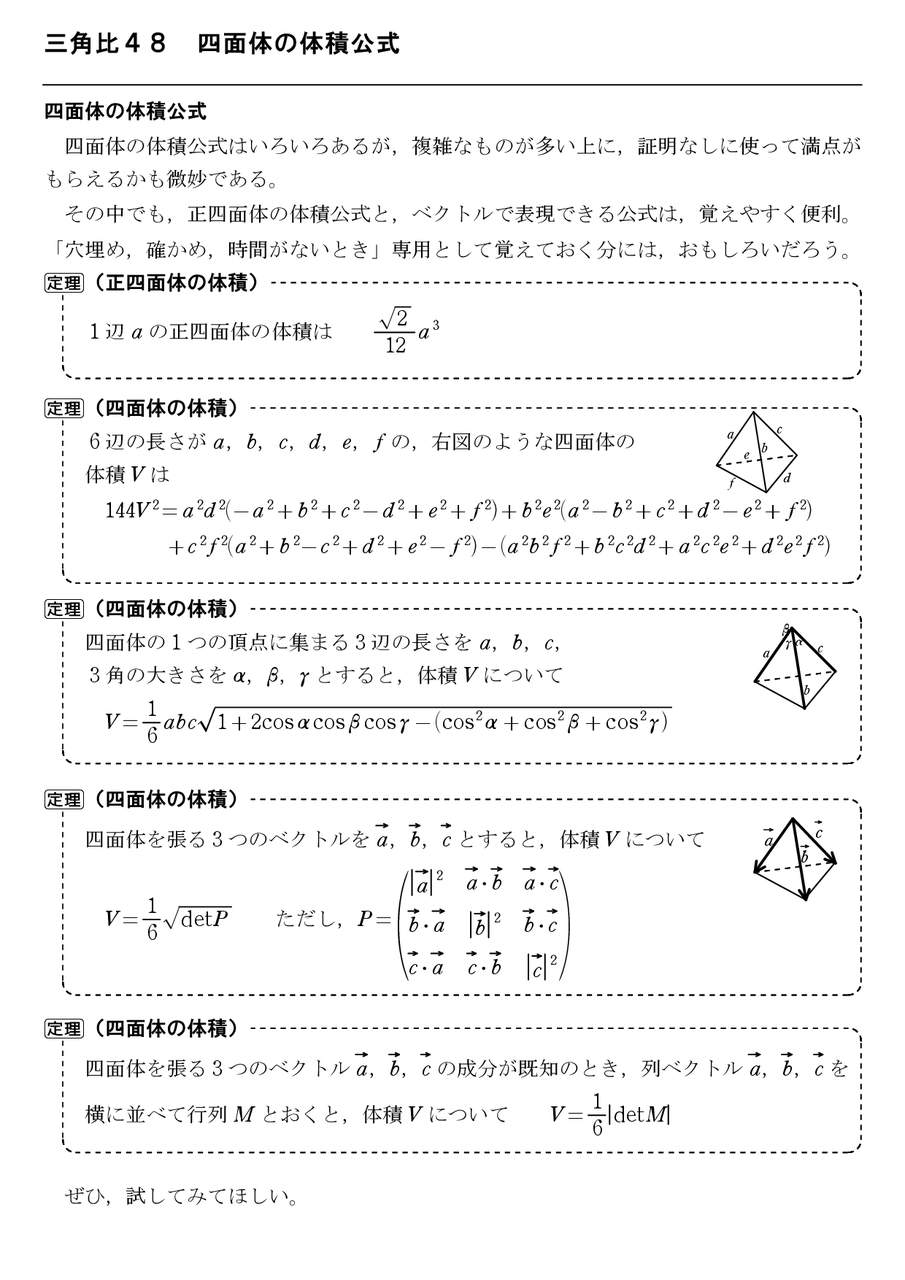


三角比 怜悧玲瓏 高校数学を天空から俯瞰する


3 B 答えが3 625だそうですが どうやってもこの答えになりません Yahoo 知恵袋
こんにちは。相城です。今回は三角錐を2つに分けたときの頂点を含む部分と,もとの三角錐との体積比の公式の紹介と証明を行ってみたいと思います。 三角錐に関する公式 下の図の三角錐で, 三角錐a-dpeと三角錐a-bqcの体積比は になる。 証明 証明今回の公式はなかなか証明が難しくて、理屈がはっきりとは理解しにくい部分もあったかもしれません。 なので、今回だけは 三角錐の体積は (三角錐の体積)= (底面積)× (高さ)× 、 表面積は面を構成している4つの三角形の面積を足し合わせれば良い のだと機械的に覚えてしまいましょう。 一方で、今回のような立体や図形の絡む問題では、展開図を持ち出すと計算三角錐の体積の求め方の公式は?? こんにちは!この記事をかいているKenだよ。タルト最高。 三角錐の体積の求め方 には公式があるよ。 底面積をS、高さをhとすると、 三角錐の体積は、 1/3 Sh になるんだ。 つまり、 (底面積)×(高さ)÷ 3 ってわけだね。



空間図形のところのこのp みたいなのってどういう意味ですか 中学数学に関する質問 勉強質問サイト
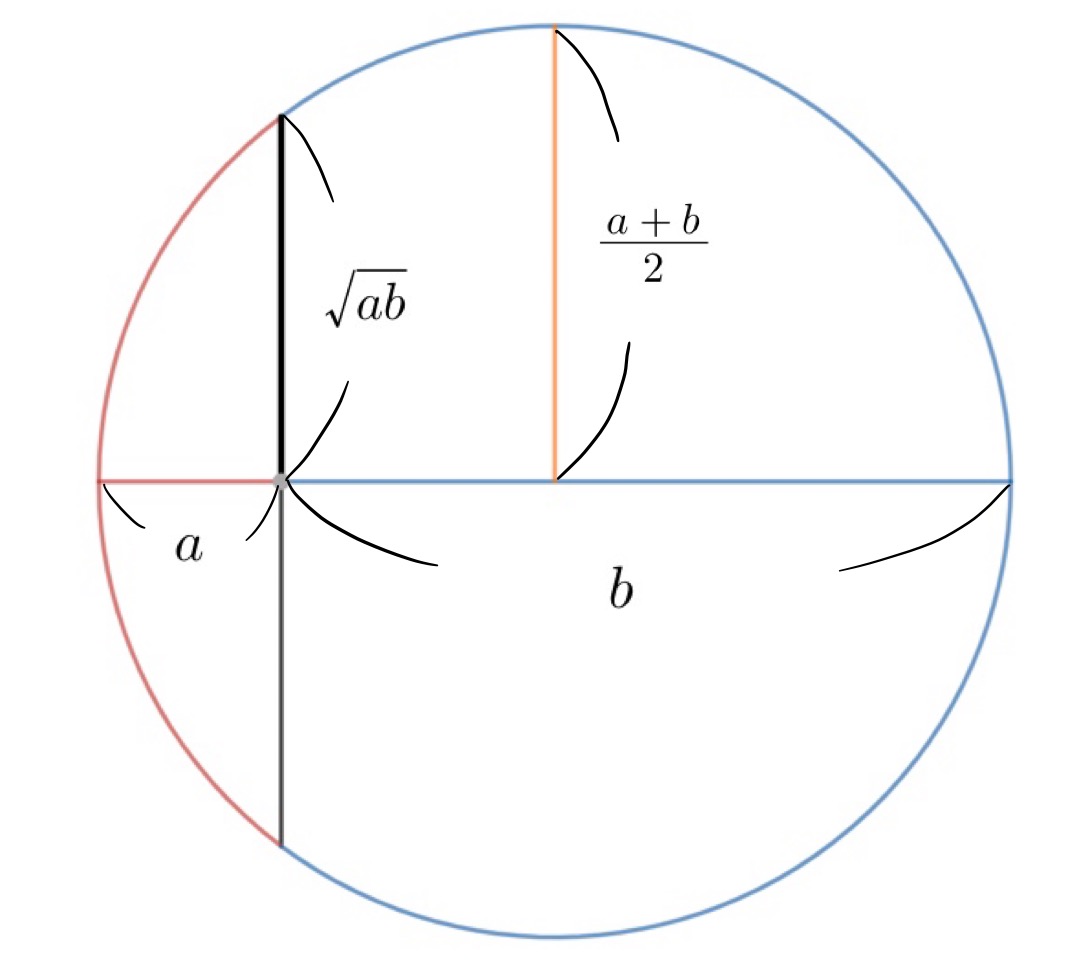


相加相乗平均の大小関係の証明や使い方 入試問題などを解説 東大医学部生の相談室
では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。 練習1 円柱 の にある部分の体積 と表面積 を求めなさい。 練習2 球 の にある部分の体積 と表面積 を求めなさい。 4.練習問題の答え 解答1 概形と底面は下の図のようになる。三角錐を一つ切り取る。さらに上下反対向きの三角錐をもう一つ切り取る。 すると残った少し妙な形の立体の体積はちょうど三角錐の体積と一致する。 したがって三角錐の体積は三角柱の体積の1/3 になる。」という記述があっ た。三角錐の体積 当HPの読者のK.S.さんより、平成24年10月10日付けで標記話題をメールで頂いた。 原点をOとし、空間上の3点A(a 1 ,a 2 ,a 3 )、B(b 1 ,b 2 ,b 3 )、C(c 1 ,c 2 ,c 3 )とする。


Saiei School Com Wp Content Uploads 17 11 C7f44ff5fe77f3e7ef673d95d84f9b6a Pdf



曲線の長さの求め方 積分公式や証明 問題の解き方 受験辞典
錐の体積の公式 三角錐,四角錐,円錐,の錐 (すい)という漢字は訓読みでは「きり」と読みます.これは,小さな穴を開けるための先のとがった工具です. 三角錐や円錐といった「錐」とは,穴をあける道具のように先の尖った立体です. では,「〇〇錐」の体積の求め方はどうだったかというと, (〇〇錐の体積) = (底面積)× (高さ)× 1 3 ( 〇〇錐の体積) = ( 底



中2数学証明ですぜひご回答をお願いします 中学数学に関する質問 勉強質問サイト



高校数学 対称面をもつ四面体の体積 受験の月
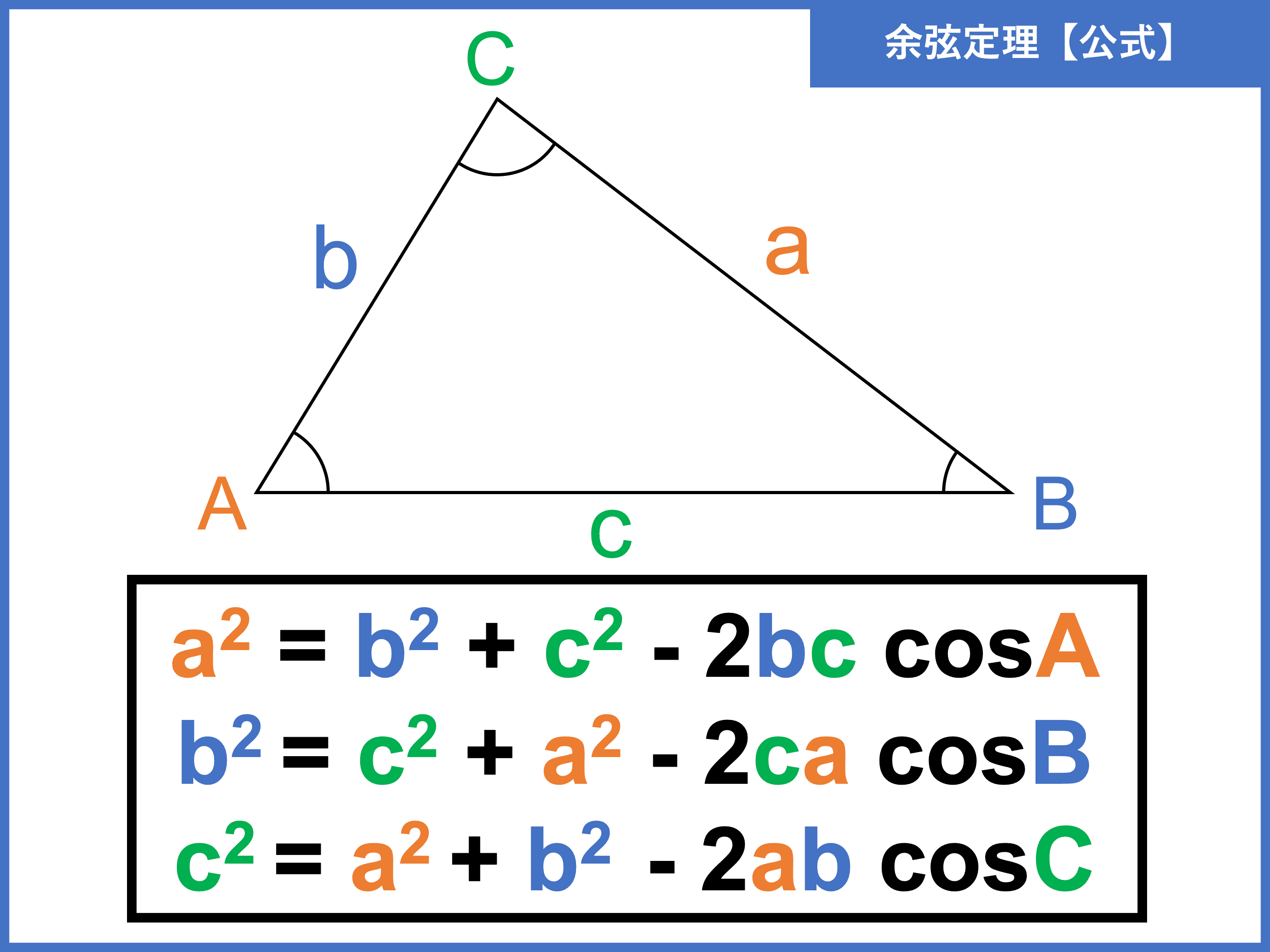


余弦定理とは 公式の覚え方や証明 計算問題の解き方 受験辞典



証明 錐の体積は何故3で割るのか小 中学生にも説明できますか Why Divide The Volume Of A Cone By 3 Can You Explain It Youtube
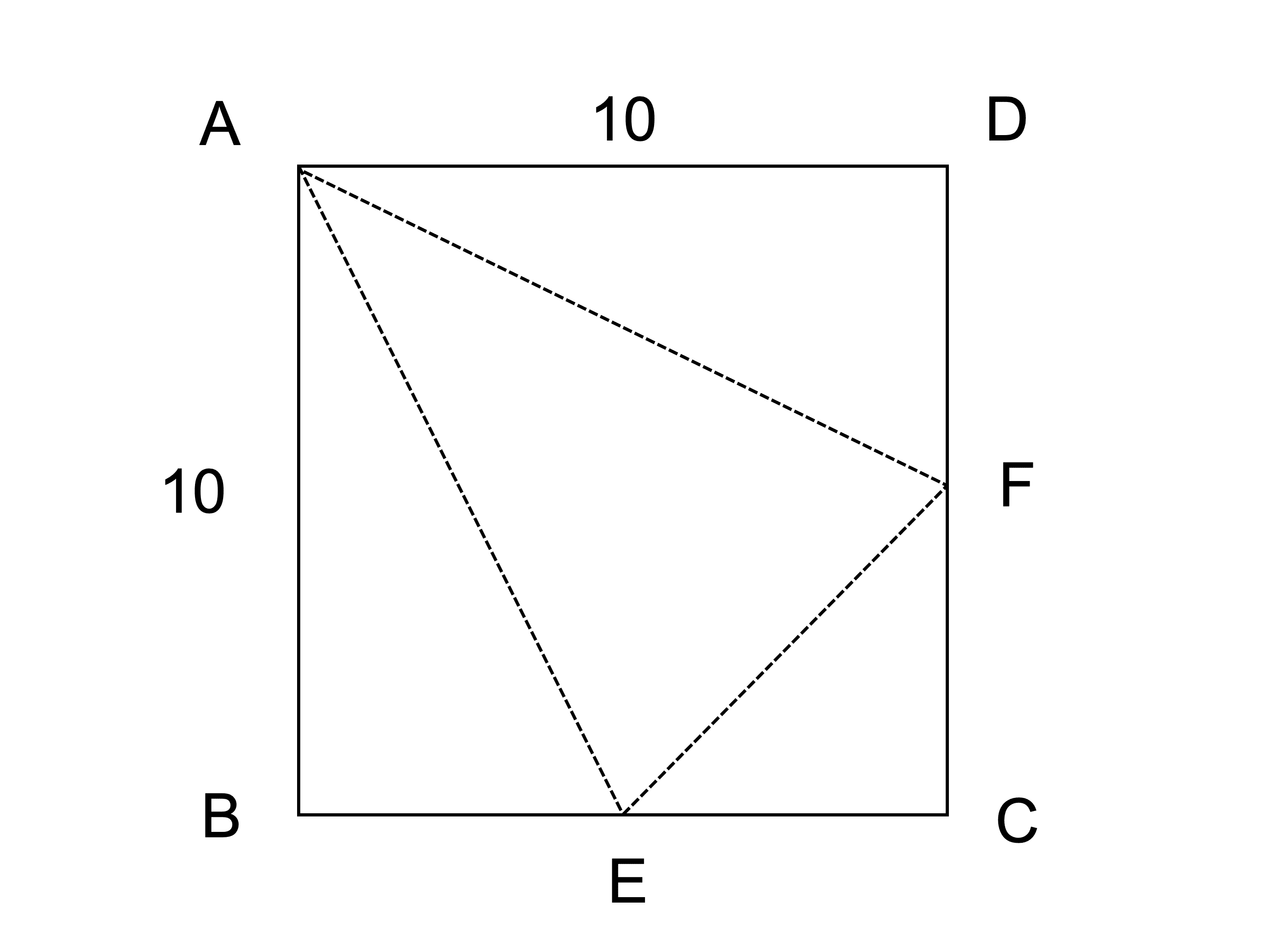


三角錐とは 体積 表面積の公式や求め方 受験辞典



数学 中学数学に関する質問 勉強質問サイト



三角比 怜悧玲瓏 高校数学を天空から俯瞰する



三角錐に関する質問 勉強質問サイト



高校数学 余角90 ー8の公式と補角180 ー8の公式の証明と強力な覚え方 三角比の等式の証明 Sin A B 2 Cosc 2など 受験の月



斜軸回転体の体積 応用編 傘型積分 おいしい数学


Core Ac Uk Download Pdf Pdf



この の問題の三角錐の高さの求め方を教えてください よろしくお願いします Clear



至急 4 が全く理解できません どうして三角錐なのかさえも解説見ても分かりません Clear


Http Www Math Chs Nihon U Ac Jp Ichihara Labo Notes 15 0622print Pdf



数学 空間図形 中学数学に関する質問 勉強質問サイト


Core Ac Uk Download Pdf Pdf



ベクトル三重積と平行六面体及び四面体の体積 身勝手な主張



三角比 怜悧玲瓏 高校数学を天空から俯瞰する



中3 三角形の相似 三角錐の体積比 日本語版 Youtube



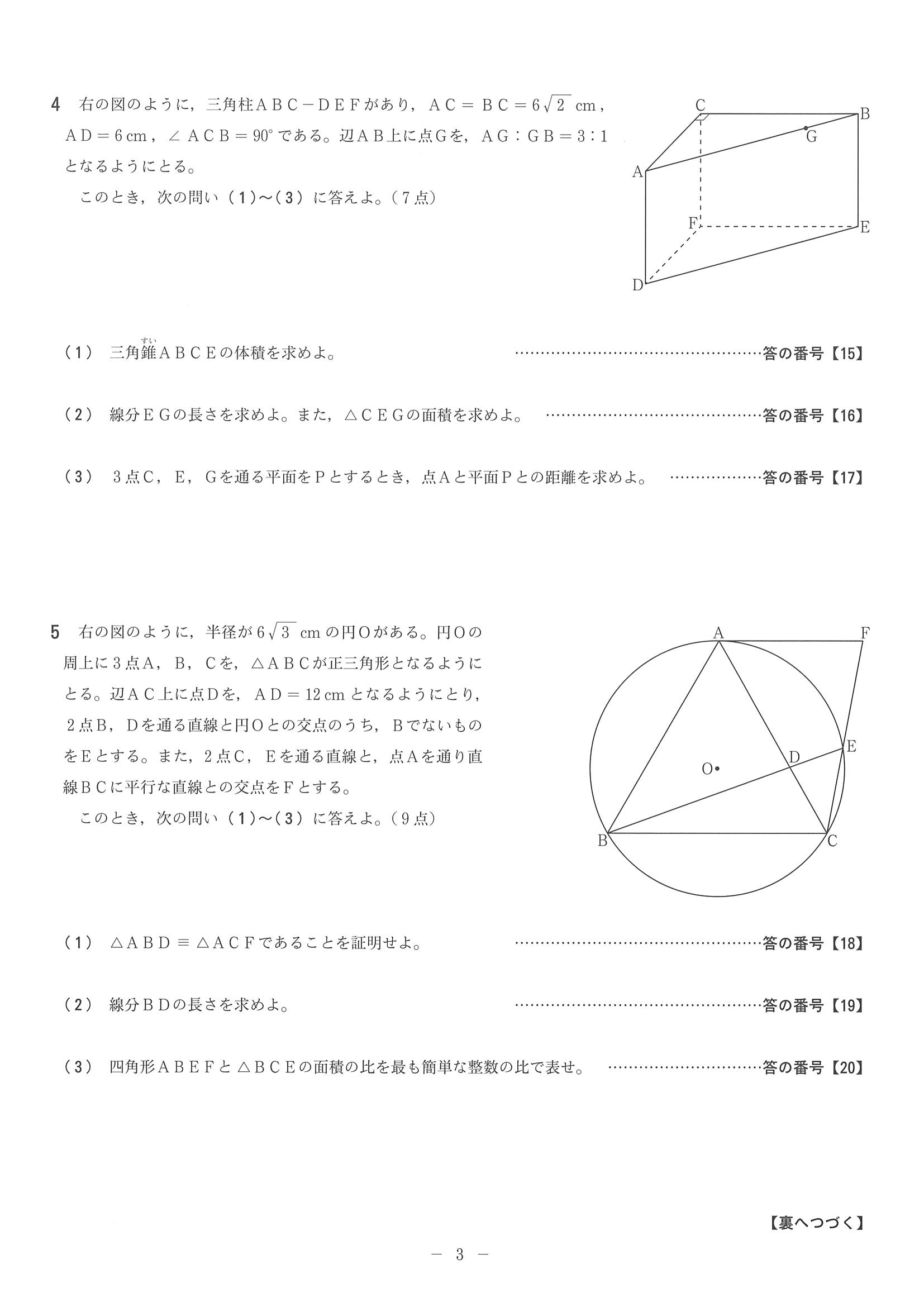
18年度 山梨県公立高校入試 標準問題 数学 問題 5 5



空間図形14 円すい台の体積 Youtube



阪大 理学研究科news 高校生向け 今年もオープンキャンパスと同日に数学教室の公開講座が開催されます 8 9 水 講師 伊藤 哲也 准教授 テーマ 三角形の面積 Vs 三角錐の体積 三角形の面積や三角錐の体積を求める公式は どうやって証明したで
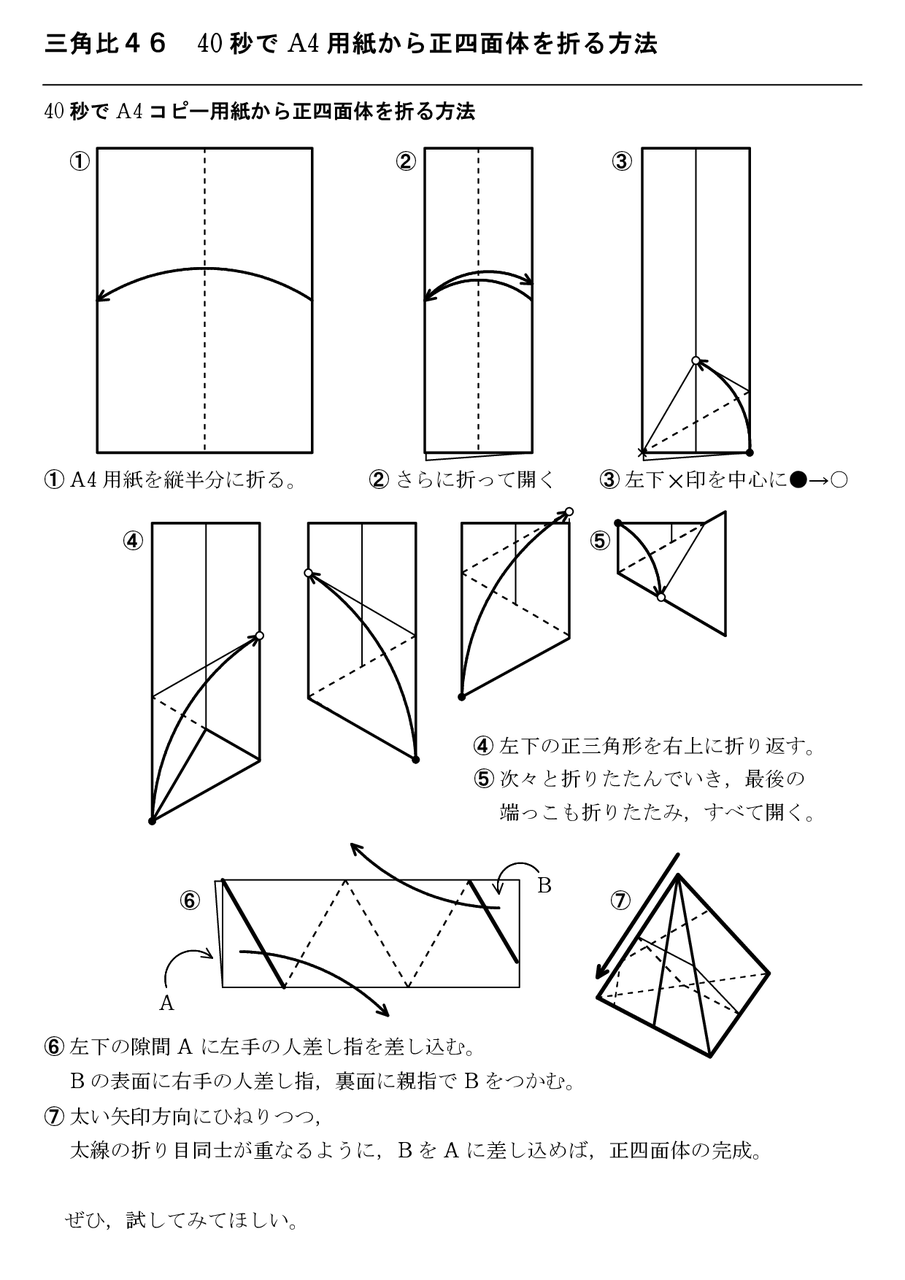


三角比 怜悧玲瓏 高校数学を天空から俯瞰する
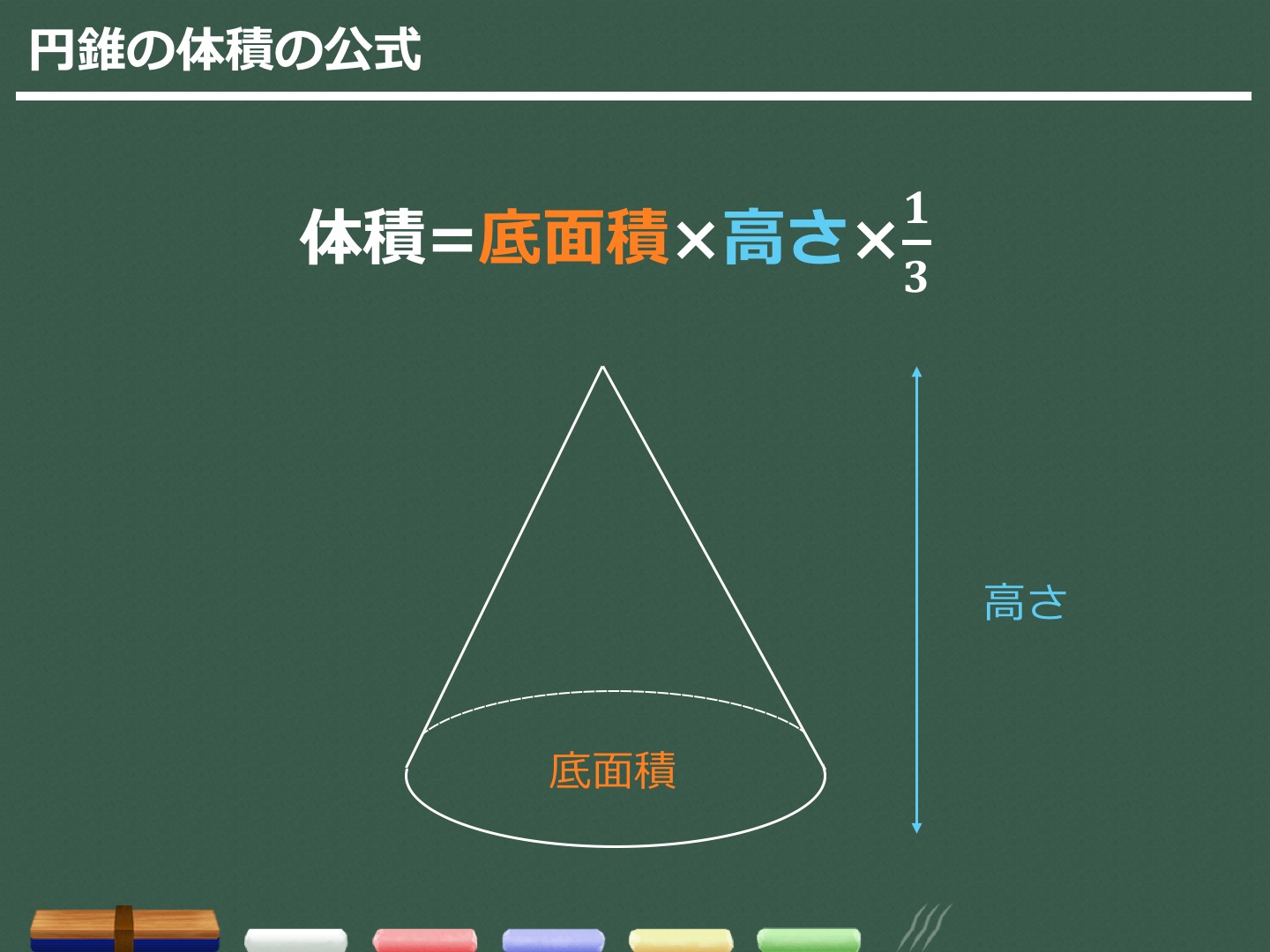


3分でわかる 円錐の体積 表面積の求め方 合格サプリ



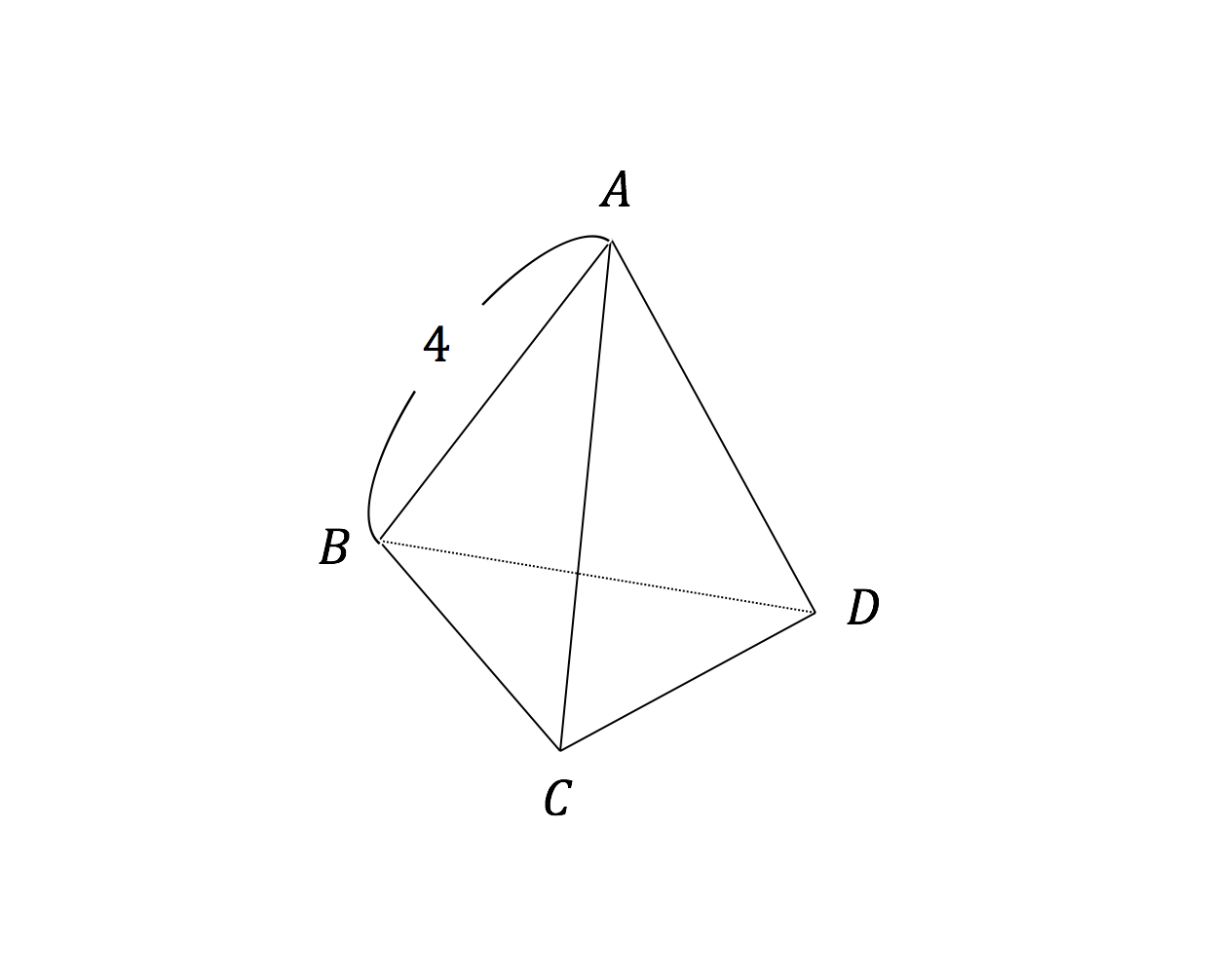
この体積の求め方で質問です 全ての辺の長さは4cmです Clear



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ


3次元面積分と体積積分



相似な図形の問題です 中学数学に関する質問 勉強質問サイト


Core Ac Uk Download Pdf Pdf



高校数学の斜め回転体の証明 1 2 Okwave
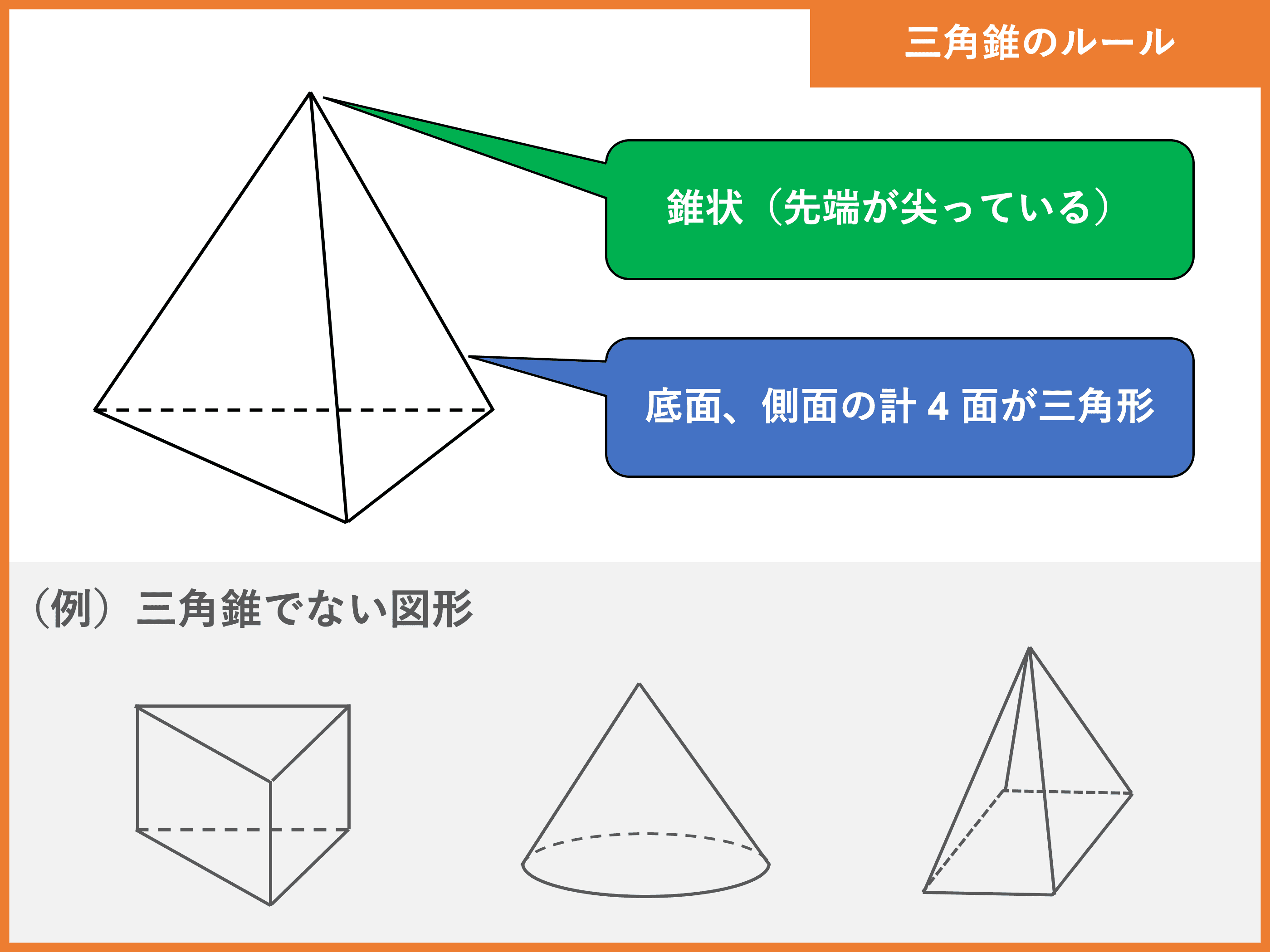


三角錐とは 体積 表面積の公式や求め方 受験辞典



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



この三角錐の体積とその求め方を教えてください よろしくお願いします Clear
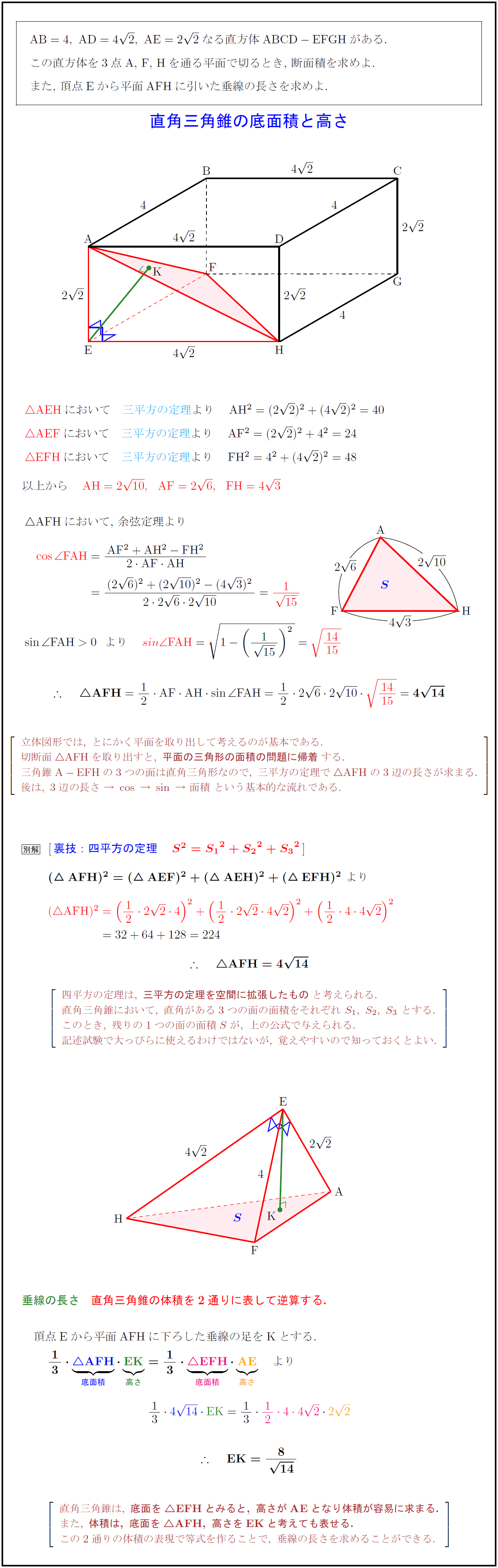


高校数学 直角三角錐 3直角四面体 の底面積と高さ 裏技 四平方の定理 受験の月


Core Ac Uk Download Pdf Pdf



数学 三角錐の体積的な感じです のみがわからないです お願いします Clear
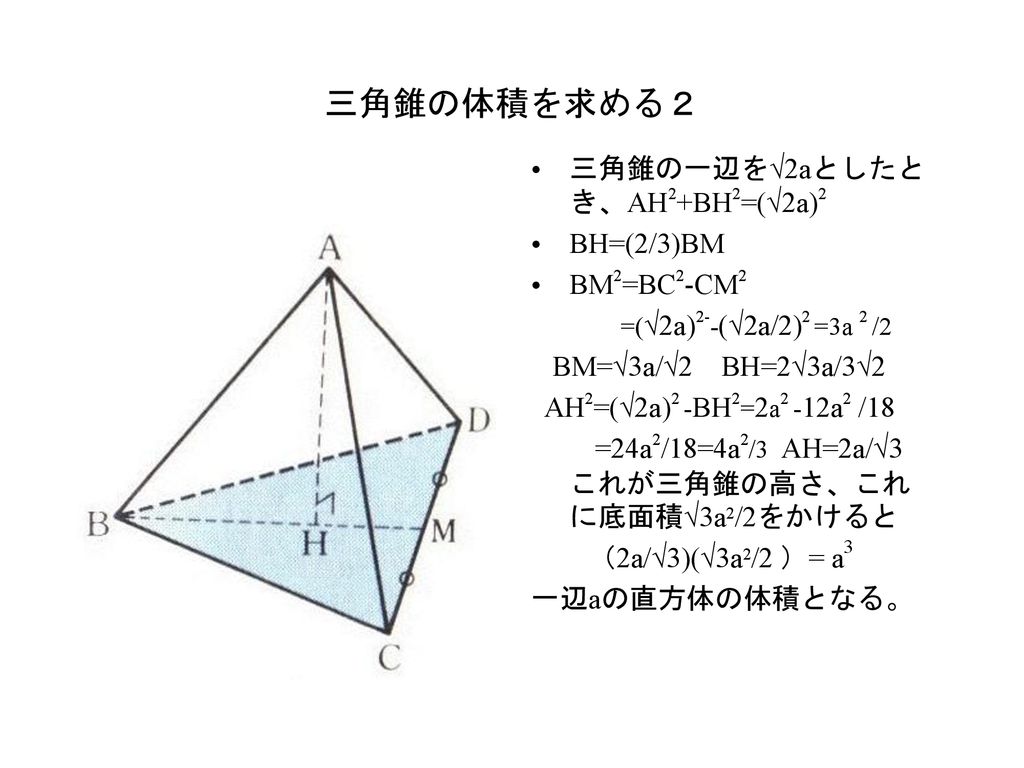


三角錐の体積 積分学まで待たねばならないか Ppt Download


2


Core Ac Uk Download Pdf Pdf
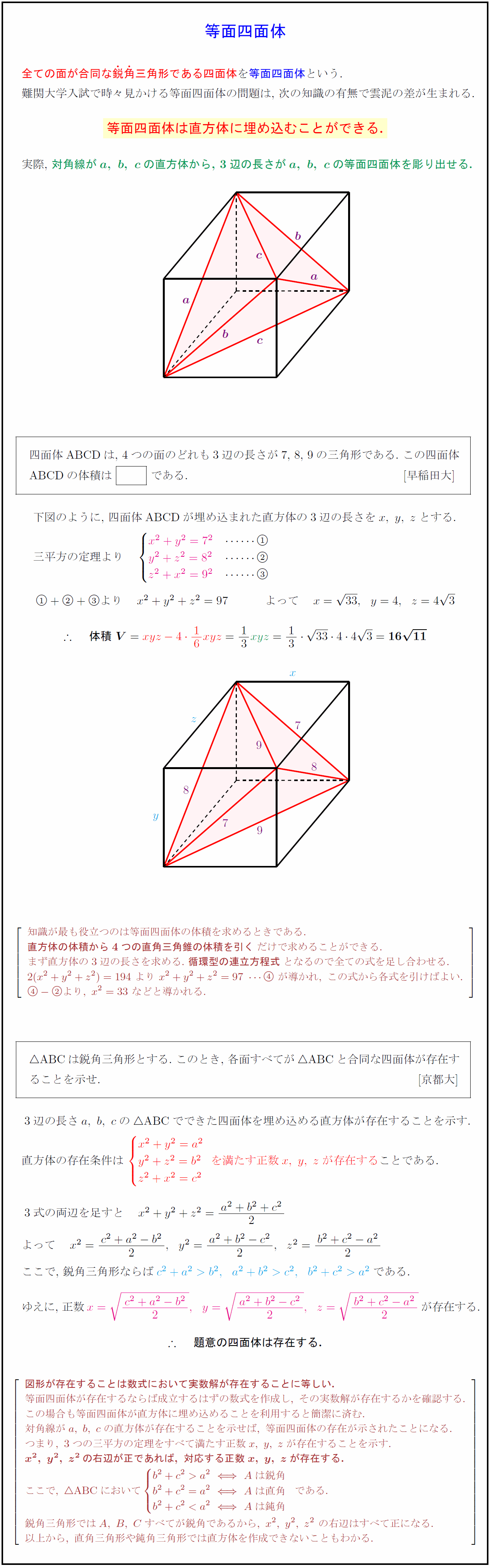


高校数学 等面四面体の体積と直方体への埋め込みと存在証明 受験の月



3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



数学 中学数学に関する質問 勉強質問サイト



電気磁気工学を学ぶ 平行六面体の体積



三角比 怜悧玲瓏 高校数学を天空から俯瞰する


悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube



三角比 怜悧玲瓏 高校数学を天空から俯瞰する


Http Www1 Center Spec Ed Jp Action Common Download Main Upload Id



電気磁気工学を学ぶ 平行六面体の体積



簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



答えを求めるときの3分の1はどこから来るのでしょうか Clear
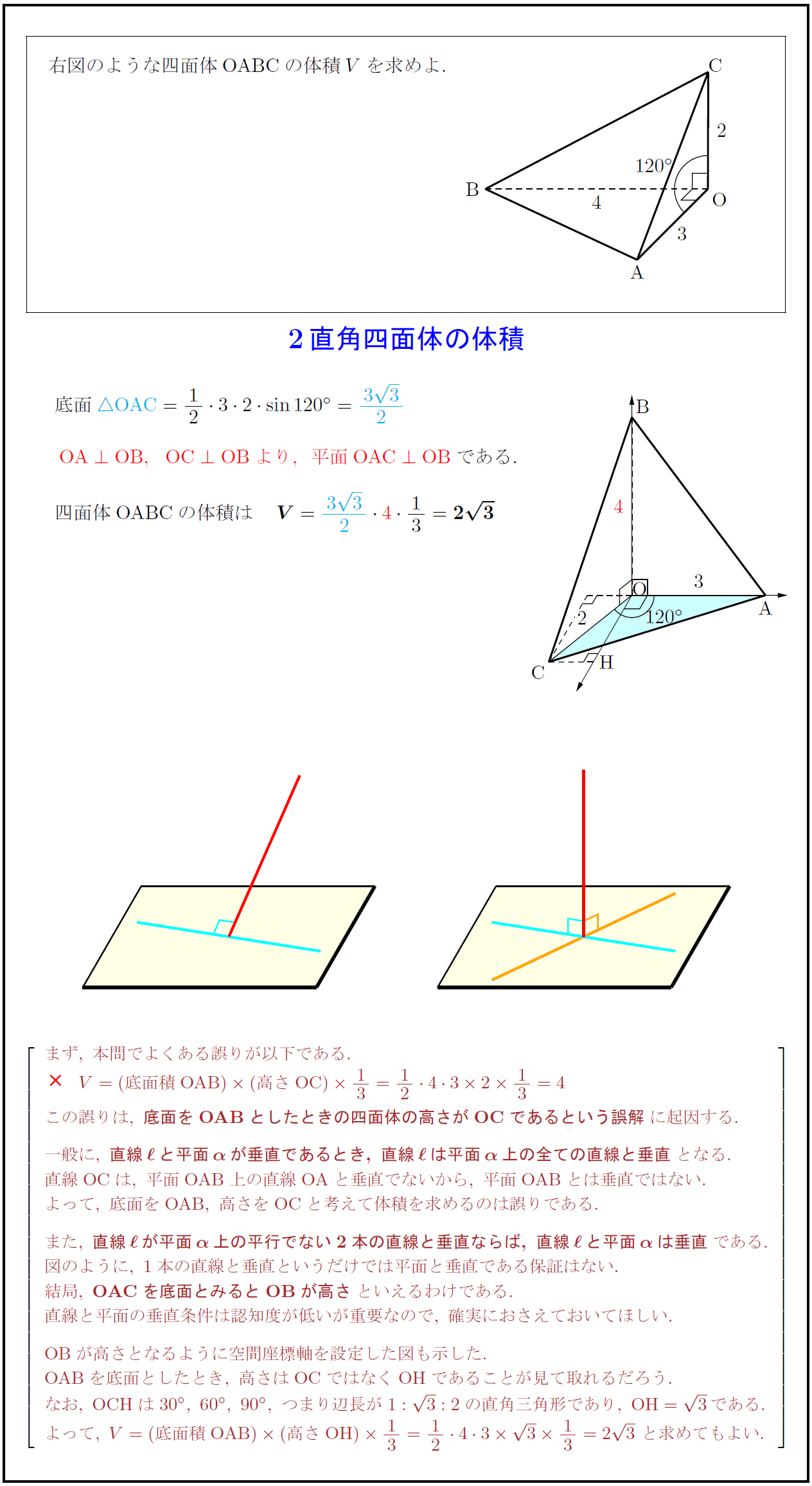


高校数学 2直角四面体の体積 直線と平面の垂直条件 受験の月



この問題は 三角錐を2個タスのでしょうか 高校数学に関する質問 勉強質問サイト



回転体に関する質問 2ページ 勉強質問サイト


三角錐とは 体積 表面積の公式や求め方 受験辞典



三角錐 Wikipedia



数学 三角錐の体積的な感じです のみがわからないです お願いします Clear


Core Ac Uk Download Pdf Pdf


Www Sakigake Jp Special H Exam Pdf Exam2 Sub21 Pdf



最も検索された 文字式の利用 問題 幼児 小学生 中学生の無料知育教材 無料学習教材プリント



高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月



円錐の体積を求める Youtube


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ


19年度 京都府公立高校入試 前期選抜 数学 問題 3 4


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典



高校数学 立体 正四面体 直円錐 表面上の最短経路 受験の月



この立体の体積の求め方教えてください お願いします Clear



至急 教えてください 答えは写真2枚目に載ってます Clear


3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ



数学 中学数学に関する質問 勉強質問サイト



正四角錐o Abcdの体積をvとして 四角錐o Pqrsの体積が Clear



円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ


三角錐とは 体積 表面積の公式や求め方 受験辞典



学校の先生がこの問題は計算をしなくても解けると言っていたのですが どのようにやれば計 Clear



高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月


Core Ac Uk Download Pdf Pdf



Ppt 三角錐の体積 積分学まで待たねばならないか Powerpoint Presentation Id



三角比 怜悧玲瓏 高校数学を天空から俯瞰する



ベクトル 三角錐の体積など 数学 大学 に関する質問 勉強質問サイト



空間図形15 断頭三角柱の体積 Youtube



正四面体とは 高さ 体積 表面積の公式や求め方 受験辞典



三角比 怜悧玲瓏 高校数学を天空から俯瞰する



3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく



三角錐の体積 積分学まで待たねばならないか Ppt Download



0 件のコメント:
コメントを投稿